The light (red rays) enters from the left, hitting the Primary Mirror M1.
M1 is concave and silvered, so it focusses the light back to the left onto the Secondary or Turning Mirror M2.
M2 is flat and at a 45 degree angle to the Optical Axis (the axis of the incoming light), so M2 bends the light at 90 degrees.
The light then enters the Eyepiece, which is moved to focus the image for the Observer (that's you).

The Data:
M1:   diameter  45.7 cm
        focal length  200 cm

M2:    diameter  7.87 cm   (perpendicular to the Optical Axis, remember M2 is tilted 45 degrees)
        focal length  infinite (it is flat--so it does not focus)

Eyepiece:  focal length  0.3 cm

Magnification:
m = f₁/f₂ = D/D'
where :     m    magnification
                f1    first focal length
                f2    second focal length
                D    diameter of the objective
                D'   diameter of the image at the eyepiece

So for our example,     200 cm / 0.3 cm = 667 Power Magnification.

It's the Focal Length of the Primary Mirror M1, divided by the Focal Length of the Eyepiece.
 Notice, we don't factor in M2, we assume it's flatness does not affect the focal length of M1

At 667 Power Magnification, let's predict the Image Diameter:

667 = 45.7 cm / D'    We switch the factors and solve for D':    45.7 cm / 667 = 0.07 cm
 

Distances:

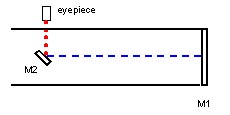
For a Newtonian, the focal length is the combination of the Blue and Red Dotted lines.
But where to put M2 ?  First decide where to put the Eyepiece.  Set it about 2.0 cm outside
the Live Optical Path.  So:

D / 2 + 2.0 cm  =  (45.7 cm / 2) + 2.0 cm = 24.85 cm from the center of M2 (or the Optical Axis).

This allows us to solve for the length from M2 to M1.

f₁ - 24.85 cm =  200 cm - 24.85 cm = 175.15 cm = M2 to M1