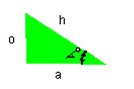
O = opposite The side that is opposite your angle <
a = adjacent The side that is next to your angle <
h = hypotenuese This is always the longest side
If you know how to use just the Basic 3 Trig Equations, you can design a great many complex 3 dimensional objects.
A very clever person once shared with me an easy way to remember the Basic Trig Equations, it has stuck with me for 25 years--so it should work for you too.
sin = o
/ h
cos = a
/ h
tan = o
/ a
"Oh
Heck,
Another
Hard
Objective
of Algebra"
Now just add the 3 functions SIN,
COSine, and TANgent to your equations.
Warning: These are good only for Right Triangles ( one angle is 90', like the corner of a square ).
Practice on the following triangle:

O = opposite The
side that is opposite your angle <
a = adjacent The
side that is next to your angle <
h = hypotenuese
This is always the longest side
For the first triangle (green on my screen), let's say:
H=6 and the angle=30 degrees
Use the 1st equation:
sin =
o / h
so sin 30' = O / 6
now isolate O by multiplying both sides by 6
sin 30' x 6 = O x 6 / 6 ( 6 / 6 = 1 so throw it away )
sin 30' x 6 = O
now use your Calculator (Windows has one in the "Accessories", go to "View" "Scientific" to get the Trig Functions).
sin 30' = 0.5 so 0.5 x 6 = 3
The side opposite the 30' angle is 3
You can find the Adjacent side with either of the other 2 equations,
or you can use Pythagorus Theorum:
A2 + B2 = C2
where C is the Hypotenuese (longest side).
A2 + 32 = 62
Isolate B by subtracting
32 from both sides of the = (equals sign).
A2 = 62 - 32 so A2 = (6 x 6) - (3 x 3) which gives 36 - 9 = 27 A2 = 27
so A = 27 0.5 ( square root of 27 ) using the Calculator: A = 5.196
Using the Trig functions, you should get the same results:
cos = a / h cos 30' = a / 6 cos 30' x 6 = a 0.866 x 6 = 5.196
or
tan = o
/ a tan 30'
= 3 / a (now transpose) a = 3 / tan
30' 3 / 0.577 = 5.196